機械学習の主要方程式まとめ

8月29日、Chizkiddが「The Most Important Machine Learning Equations: A Comprehensive Guide」と題した記事を公開した。この記事では、機械学習を支える主要な数学的方程式について詳しく紹介されている。

以下に、その内容を簡潔に紹介する。詳しくは原文を参照していただきたい。

1. 確率と情報理論

ベイズの定理

方程式

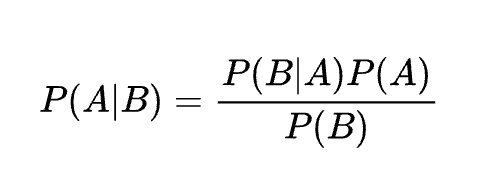
説明
新しい証拠 $B$ に基づいて仮説 $A$ の確率を更新する手法。分類やベイズ最適化に利用される。

Python実装

def bayes_theorem(p_d, p_t_given_d, p_t_given_not_d):
    p_not_d = 1 - p_d
    p_t = p_t_given_d * p_d + p_t_given_not_d * p_not_d
    return (p_t_given_d * p_d) / p_t

print(bayes_theorem(0.01, 0.99, 0.02))  # 出力: 0.3333

エントロピー

方程式

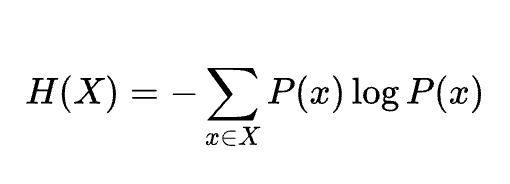
説明
確率分布の不確実性を定量化する。情報利得や決定木の分岐基準に使われる。

Python実装

import numpy as np

def entropy(p):
    return -np.sum(p * np.log(p, where=p > 0))

print(entropy(np.array([0.5, 0.5])))  # 公平なコイン → 0.693
print(entropy(np.array([0.9, 0.1])))  # 偏ったコイン → 0.469

同時確率・条件付き確率

方程式

同時確率

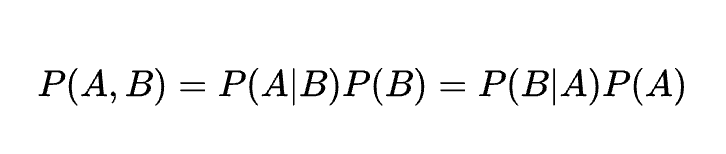
条件付き確率

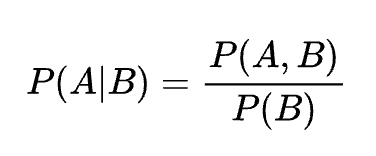
説明
複数の事象が同時に起こる確率や、ある条件下での確率を示す。ナイーブベイズや確率モデルで利用。

Python実装

from sklearn.naive_bayes import GaussianNB
import numpy as np

X = np.array([[1, 2], [2, 3], [3, 4], [4, 5]])
y = np.array([0, 0, 1, 1])
model = GaussianNB().fit(X, y)
print(model.predict([[2.5, 3.5]]))  # 出力: [1]

KLダイバージェンス

方程式

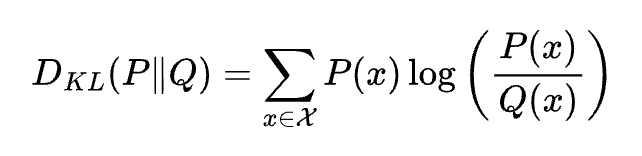
説明
分布 $P$ が分布 $Q$ からどれだけ乖離しているかを測定する。非対称な距離尺度。VAEや生成モデルで使用される。

Python実装

P = np.array([0.7, 0.3])
Q = np.array([0.5, 0.5])
kl_div = np.sum(P * np.log(P / Q))
print(kl_div)  # 出力: 0.082

クロスエントロピー

方程式

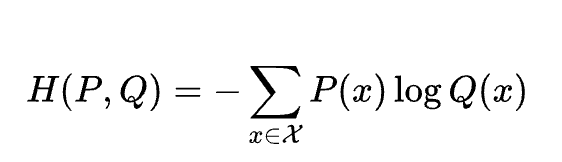
説明
真の分布 $P$ と予測分布 $Q$ の差異を測定。分類モデルの損失関数として利用される。

Python実装

y_true = np.array([1, 0, 1])
y_pred = np.array([0.9, 0.1, 0.8])
cross_entropy = -np.mean(y_true * np.log(y_pred) + (1-y_true)*np.log(1-y_pred))
print(cross_entropy)  # 出力: 0.164

2. 線形代数

線形変換

方程式

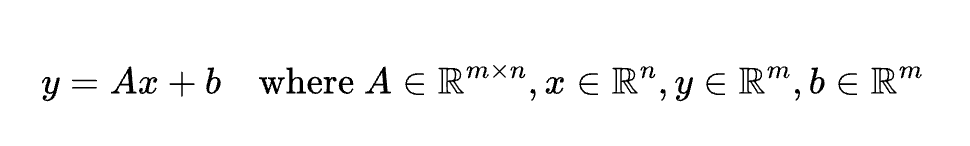
説明
入力ベクトルを行列 $A$ とバイアス $b$ で変換。ニューラルネットの基礎演算。

Python実装

A = np.array([[2, 1], [1, 3]])
x = np.array([1, 2])
b = np.array([0, 1])
print(A @ x + b)  # 出力: [4 7]

固有値・固有ベクトル

方程式

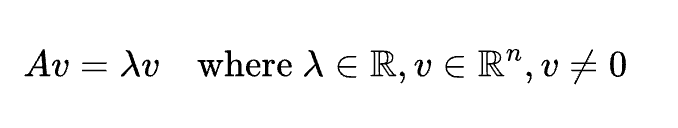
説明
行列の作用を保存するベクトルと、そのスケーリング量。PCAの基盤。

Python実装

A = np.array([[4, 2], [1, 3]])
eigenvalues, eigenvectors = np.linalg.eig(A)
print(eigenvalues)  
print(eigenvectors)

特異値分解 (SVD)

方程式

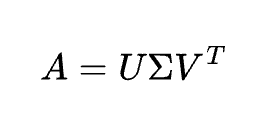
説明
行列を直交行列と特異値に分解。次元削減や推薦システムで利用。

Python実装

A = np.array([[1, 2], [3, 4], [5, 6]])
U, S, Vt = np.linalg.svd(A)
print(S)

3. 最適化

勾配降下法

方程式

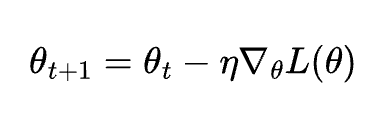
説明
損失関数 $L$ の勾配に基づいてパラメータを更新。

Python実装

def gradient_descent(X, y, lr=0.01, epochs=1000):
    m, n = X.shape
    theta = np.zeros(n)
    for _ in range(epochs):
        gradient = (1/m) * X.T @ (X @ theta - y)
        theta -= lr * gradient
    return theta

誤差逆伝播法

方程式

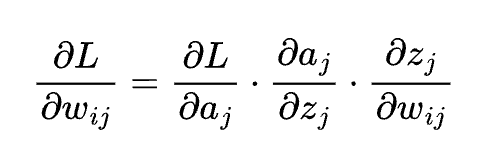
説明
チェインルールで勾配を効率的に計算し、深層学習を可能にする。

Python実装

import torch
import torch.nn as nn

model = nn.Sequential(nn.Linear(2, 1), nn.Sigmoid())
loss_fn = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

X = torch.tensor([[0., 0.], [1., 1.]])
y = torch.tensor([[0.], [1.]])
optimizer.zero_grad()
loss = loss_fn(model(X), y)
loss.backward()
optimizer.step()

4. 損失関数

平均二乗誤差 (MSE)

方程式

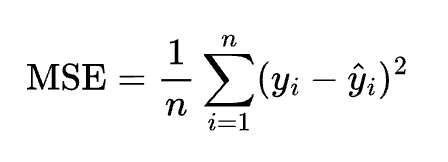
説明
回帰における誤差を測定。大きな誤差をより強く罰する。

Python実装

y_true = np.array([1, 2, 3])
y_pred = np.array([1.1, 1.9, 3.2])
print(np.mean((y_true - y_pred)**2))  # 出力: 0.01

5. 先端的概念

拡散過程

方程式

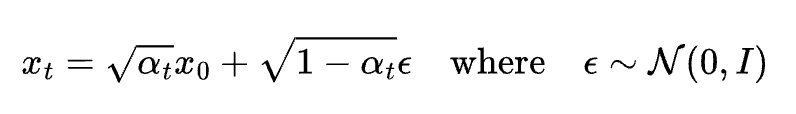
説明
データにノイズを加える生成モデルの基盤。

Python実装

import torch
x_0 = torch.tensor([1.0])
alpha_t = 0.9
noise = torch.randn_like(x_0)
x_t = torch.sqrt(torch.tensor(alpha_t)) * x_0 + torch.sqrt(torch.tensor(1-alpha_t)) * noise
print(x_t)

畳み込み演算

方程式

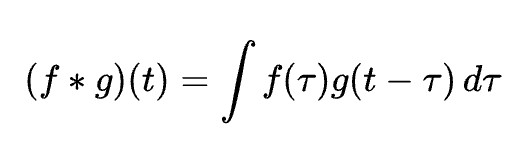
説明
画像処理で特徴抽出を行う操作。CNNの基礎。

Python実装

import torch.nn as nn
import torch
conv = nn.Conv2d(1, 1, kernel_size=3)
image = torch.randn(1, 1, 28, 28)
print(conv(image).shape)  # 出力: [1, 1, 26, 26]

ソフトマックス関数

方程式

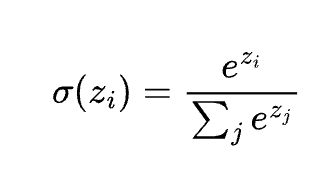
説明
スコアを確率分布に変換。多クラス分類で利用。

Python実装

z = np.array([1.0, 2.0, 3.0])
softmax = np.exp(z) / np.sum(np.exp(z))
print(softmax)  # 出力: [0.090, 0.245, 0.665]

アテンション機構

方程式

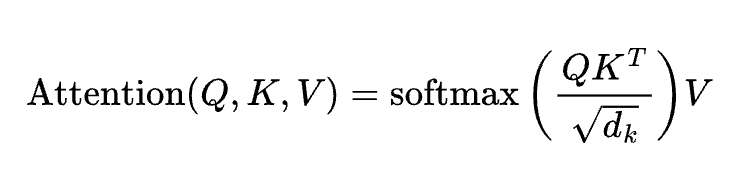
説明
クエリとキーの類似度に基づいてバリューを重み付け。Transformerの中核。

Python実装

def attention(Q, K, V):
    d_k = Q.size(-1)
    scores = (Q @ K.T) / torch.sqrt(torch.tensor(d_k, dtype=torch.float32))
    attn = torch.softmax(scores, dim=-1)
    return attn @ V

Q = torch.tensor([[1., 0.], [0., 1.]])
K = torch.tensor([[1., 1.], [1., 0.]])
V = torch.tensor([[0., 1.], [1., 0.]])
print(attention(Q, K, V))

結論

この記事は、機械学習の基盤となる数式を網羅的に整理し、それぞれに数式・説明・Python実装例を付与している。理論から実装まで一貫して理解できる点が特徴である。

詳細はThe Most Important Machine Learning Equations: A Comprehensive Guideを参照していただきたい。