Haskellerのためのモノイド完全ガイド

Haskellにおけるモノイドについて解説記事を書いてみた。他の言語でも通用する話があるかもしれないし、ないかもしれない。

モノイドとは

モノイドとは、ざっくり言うと「くっつける」演算ができる対象のことである。例えば、文字列やリストの連結、数の足し算や掛け算は「くっつける」演算の一種である。

モノイドには「くっつける」演算の他にもう一つ条件があって、モノイドは「くっつけても何も起こらない値」を持っていなければならない。例えば、文字列の場合は空文字列、リストの場合は空リスト、数の足し算の場合は0、掛け算の場合は1、という具合である。

というわけで、文字列、リスト、数の足し算、数の掛け算はいずれもモノイドの具体例である。ただし、同じ数の集合（整数、など）を考えていても、演算が異なる（足し算 vs 掛け算）場合は、異なるモノイドとみなす。

モノイドの定義をちゃんと書くと、モノイドとは集合 \(M\) および

くっつける演算（以後、この演算を \(\diamond\) によって \(a \diamond b\) と書くことにする）
- この演算は結合的である。つまり任意の \(a\), \(b\), \(c\) に対して \((a\diamond b)\diamond c=a\diamond(b\diamond c)\) が成り立つ。
くっつけても何も起こらない値（以後、この値を \(e\) で書くことにする）
- つまり、任意の \(a\) に対して \(a\diamond e=e\diamond a=a\) が成り立つ。
- この「何も起こらない値」のことを、単位元という。

の組 \((M,\diamond,e)\) のことである。「結合的」とかごちゃごちゃ書いたが、「くっつける」という直観を堅苦しい言葉で書いただけである。

モノイドじゃない例を挙げておくと、例えば数の引き算は結合的でない（例えば \((1-2)-3\ne 1-(2-3)\)）ので、数およびその引き算の組はモノイドではない。

モノイドの具体例は、すでに文字列、リスト、数の足し算、数の掛け算を挙げた。この他にもプログラミングにおいてモノイドの具体例はたくさん登場する。それらの例は追い追い見ていこう。

HaskellとMonoidクラス

Haskellには、モノイドを統一的に扱えるMonoidクラスが用意されている。例えば、文字列 String やリスト [a] は Monoidのインスタンスである。一方で、数に関しては「くっつける」演算が「足し算」「掛け算」とあって万人が納得する「これだ！」というものがないので、 Int や Double などの具体的な数の型はMonoidのインスタンスにはなっていない（この辺の話は後述する）。

-- Monoid型クラスの定義（説明用。現実のGHCのものとはちょっと違うので注意）
class Monoid a where
  (<>) :: a -> a -> a  -- 「くっつける」演算
  mempty :: a          -- 「くっつけても何も起こらない値」

さて、モノイドという抽象概念がMonoidという型クラスになっていると何が嬉しいか。色々答え方はあるだろうし、この記事の中でもいくつかの回答を提示するが、まずは「様々な文字列型に対して同じ連結演算子 <> を適用できる」という点を挙げておきたい。

Haskellと文字列と連結演算子

一旦モノイドは棚に上げて、Haskellの文字列の話をしよう。

Haskellにおける文字列型は String である。文字列の連結はリストと同じく ++ 演算子によって行える。

……Haskell初心者には上記の説明で良いだろうが、中級者以上にはそれでは不十分だ。

Haskellの String 型の実体は文字のリスト [Char] であり、あまり効率が良くない。もっと効率の良い文字列型として、 Data.Text の Text 型や、 Data.ByteString の ByteString 型がある。さらにいうと、その Lazy 版もあって正直カオスである。

型が色々あるということは、文字列操作関数もその分だけあるということである。Text 型の文字列連結は Data.Text.append を使うし、 ByteString 型の文字列連結は Data.ByteString.append を使う。Text 型で表される文字列の各文字に変換（大文字にする、など）を施したかったら Data.Text.map を使うし、 ByteString 型の各文字を変換したかったら Data.ByteString.map を使う。

しかし、サクッとコードを書きたいときに「この文字列は Text だから Data.Text.append で連結して、こっちは ByteString だから Data.ByteString.append で……」ということを考えるのは面倒である。細々とした文字列操作はともかく、文字列連結くらいは共通の演算子があっても良いのではないか。

素性の異なる型（この場合は String と Text、それから ByteString）に対して同じ名前の演算子や関数を定義するには、Haskellでは型クラスという機構を使う。ということで、例えば

class StringConcat a where
  (+++) :: a -> a -> a  -- 連結演算
  emptyString :: a     -- 空文字列

instance StringConcat String where ...
instance StringConcat Data.Text.Text where ...
instance StringConcat Data.ByteString.ByteString where ..

という風にすれば良い。すれば良いのだが……。

この StringConcat クラスの定義を見ると、「文字列」固有の部分がまるでない。そう、これはただのモノイドである。だったらわざわざ文字列連結用の型クラスなんて定義しなくても、モノイドの連結演算子 <> （Monoidクラス）を文字列連結演算子として使えるようにすれば良いじゃん！

というわけで、Haskellにおける Monoid クラスの一つの存在意義は、「乱立する文字列型に対して、文字列連結を同じ演算子 <> によって行えるようにする」ことだと言える。

モノイドの例

ここからはひたすらモノイドの例を見ていく。ちょっと長いので、飽きたら次のセクションに進んでもらって構わない。

文字列 (String, Text, ByteString)

すでに説明したように、文字列（文字列と連結演算）はモノイドの代表例である。

（数学風に言えば、（有限長の）文字列というのは文字の集合で生成される自由モノイドなので、文字列というのは最も典型的なモノイド、と言えるかもしれない。）

Haskellにはいくつも文字列型があるが、いずれも <> で連結できる。というわけで、Haskellにおける文字列連結演算子は <> である、と言って良いだろう。

数：足し算と掛け算 (Sum, Product)

最初の方に述べたように、数の足し算や掛け算もモノイドの例となる。（浮動小数点数の場合は丸めがあるから云々、という話はこの記事では無視する）

ただ、Haskellの仕組み上、 Int という一つの型に対して複数の Monoid インスタンスを定義することはできない。

-- こういうのはダメ：

instance Monoid Int where
  -- 足し算に関するモノイド
  (<>) = (+)

instance Monoid Int where
  -- 掛け算に関するモノイド
  (<>) = (*)

ではどうするか、というと、演算ごとに newtype で別名を用意してやる。つまり

newtype Sum a = Sum { getSum :: a }
instance (Num a) => Monoid (Sum a) where
  Sum x <> Sum y = Sum (x + y)
  mempty = 0

newtype Product a = Product { getProduct :: a }
instance (Num a) => Monoid (Product a) where
  Product x <> Product y = Product (x * y)
  mempty = 1

と定義すれば、 Int の足し算に関するモノイドは Sum Int 、掛け算に関するモノイドは Product Int という風に、適宜使い分けられる。この Sum 型や Product 型は Data.Monoid モジュールですでに定義されているので、ユーザーが新たに定義する必要はない。

さて、newtype まで持ち出して数を Monoid のインスタンスにするメリットとは何なのか？普通に + や * を使うのではダメなのか？

確かに、普通に数の足し算をする上で getSum (Sum 1 <> Sum 2) などと書くHaskellプログラマーはいない。普通に 1 + 2 と書いた方がタイプ数も少ないし、誰にとってもわかりやすい。

だからと言って、 Sum や Product 型が全く存在意義がないというわけではない。詳しくは後述する。

Bool: 論理積と論理和 (All, Any)

Bool 型の論理積 && と論理和 || もそれぞれモノイドとなる。一つの型に複数の Monoid インスタンスを定義できないのはさっき書いた通りで、やはりこれも別名が定義されている：

newtype All = All { getAll :: Bool }
instance Monoid All where ... -- (&&) に関するモノイド

newtype Any = Any { getAny :: Bool }
instance Monoid Any where ... -- (||) に関するモノイド

型の名前は And/Or ではなくて All/Any である。複数の値をくっつけた際に、 && の方は「すべて (all)」真の場合に真となり、 || は「いずれか (any)」が真の場合に真となる。

まあ論理積や論理和を普通に使う分には && や || をそのまま使えば良い。All 型や Any 型の存在意義は……やはり後述する。

自分自身への関数 `a -> a` (Endo)

関数合成 . も結合法則 (f . g) . h = f . (g . h) が成り立つし、モノイドっぽい雰囲気がある。ただ、一般の関数型 a -> b はモノイドではない。モノイドになるのは、引数と返り値の型が同じ場合 a -> a である。

こういう「自分自身への関数」 a -> a は、関数合成に関してモノイドとなる。モノイドの単位元は「入力をそのまま返す」恒等関数 id :: a -> a である。

ただ、Haskellの制限として a -> a という型そのものを Monoid のインスタンスにすることはできない（instance Monoid (a -> a) とは書けない）。この場合もやはり newtype が用意されていて、

newtype Endo a = Endo { appEndo :: a -> a }
instance Monoid (Endo a) where
  Endo f <> Endo g = Endo (f . g)
  mempty = Endo id

という風になっている。

😾「だがちょっと待ってくれ。関数合成の方法は f . g だけじゃなくて g . f でも良いのでは？後者の方が Endo f <> Endo g と書いたときに『左から右へ処理される』感があって好きなのだが」

そう、それは一理ある。ただ、これに関する答えはもう少し待って欲しい。（待ちきれない人は Dual の解説へ飛べ✈️🙀）

ちなみに、「Endo」という名前は数学用語の endomorphism（自己準同型）から来ており、ライブラリー作者が数学オタクであることがうかがえる。遠藤さんとかじゃないよ

Maybe, First, Last

Maybe 型もモノイドになる。Maybe のモノイド定義の方法もいくつか考えられる。

まず、 Nothing が単位元になるようにモノイド演算を

Nothing <> Nothing = Nothing
Nothing <> Just x = Just x
Just x <> Nothing = Just x

と定義することに異論はないだろう。では Just 同士の演算はどう定義したら良いか。

Just x <> Just y = ???

この定義の方法はすぐに思いつくものとして3通りくらい考えられる：

Maybe の中身もモノイドだと仮定して、 Just x <> Just y = Just (x <> y) とする。
左側を返す： Just x <> Just y = Just x
右側を返す： Just x <> Just y = Just y

これらはいずれも、モノイドとしての性質を満たす。

Haskellでは、Maybe の Monoid インスタンスとしては「1. Maybe の中身もモノイドだと仮定して、〜」が採用されていて、2. と 3. に関してはそれぞれ Data.Monoid に First, Last という newtype ラッパーが用意されている。

例えば、 First Nothing <> First (Just 1) <> First Nothing <> First (Just 3) を計算すると First (Just 1) が得られる。「くっつけた」値のうち、一番初めの（なるべく Nothing ではない）ものを返すから First という名前がついている。

（記憶力に余裕のある読者諸氏は、 Maybe のモノイドインスタンスの定義、つまり「1. Maybe の中身もモノイドだと仮定して〜」において中身のモノイドの単位元を利用していないことを覚えておいて欲しい）

Max, Min: 大きい方と小さい方

みなさん、max関数やmin関数は使ったことがあるかと思う。整数や実数のように、大小関係が定まった対象のうち、大きい方／小さい方を返す関数だ。

このmax関数とmin関数に関しては、

\(\max\{a,\max\{b,c\}\}=\max\{{\max\{a,b\}},c\}\)
\(\min\{a,\min\{b,c\}\}=\min\{{\min\{a,b\}},c\}\)

という関係が成り立つ。これはどことなくモノイド演算の結合法則 \(a\diamond(b\diamond c)=(a\diamond b)\diamond c\) に似ているのではないだろうか。よりわかりやすいようにHaskellの中置記法を使って書くと、

a `max` (b `max` c) = (a `max` b) `max` c
a `min` (b `min` c) = (a `min` b) `min` c

となる。これは紛れもない結合法則じゃないか！

ただ、これだけで max 関数と min 関数がモノイドである、とは言えない。モノイドの定義には「何もしない」単位元が含まれるが、 max や min に関して「何もしない」値とはどういうものだろうか？

maxに関して「何もしない」値 \(e\) というのは、つまり

任意の \(a\) に対して \(\max\{a,e\}=a\)

となる値のことである。\(\max\{a,e\}=a\) というのはつまり \(e\) が \(a\) 以下である \(e\le a\) ということなので、\(e\) は「任意の \(a\) に対して、\(a\) 以下」ということになる。そう、 \(e\) はその型が取りうる最小値のことなのだ。

minに関しても同様に考えると、モノイドとしての単位元は、その型が取りうる最大値であることがわかる。

というわけで、全順序が定まった型に対して、最小値が存在するときにmaxはモノイドとなり、最大値が存在するときにminはモノイドとなる。

Haskellでmax/minをMonoidとして取り扱うには例によって newtype を使う。Haskell標準の型クラスでは、最大値・最小値はひっくるめて Bounded 型クラスで表されるので、定義は

-- module Data.Semigroup 内
newtype Max a = Max { getMax :: a }
instance (Ord a, Bounded a) => Monoid (Max a) where
  Max x <> Max y = Max (max x y)
  mempty = minBound

newtype Min a = Min { getMin :: a }
instance (Ord a, Bounded a) => Monoid (Min a) where
  Min x <> Min y = Min (min x y)
  mempty = maxBound

となっている。（残念ながら、最大値はなくて最小値だけがある（例：自然数）状況では Max モノイドを使うことはできない）

なお、 maxBound や minBound じゃなくて、特別な値（Just x に対する Nothing みたいな）を単位元としたい、という場合には……この記事の後の方の「半群」の部分を読んでいただきたい。

Ordering: 辞書式順序

Haskellでは compare 関数による比較演算の結果は Ordering 型によって帰ってくる。Ordering 型は3つの値を持ち、それぞれ

compare a b == LT: \(a<b\) (less than)
compare a b == EQ: \(a=b\) (equal)
compare a b == GT: \(a>b\) (greater than)

である。

この Ordering にもモノイド演算が定義できる。Haskell風に定義をかけば、こうだ：

LT <> y = LT
EQ <> y = y
GT <> y = GT

この演算が結合法則を満たすことはちょっと考えればわかる。このモノイド演算の単位元は EQ である。

で、定義できるのはよいが、これは何の役に立つのか？

これには実用的な使い道があって、辞書式順序を実装するのに使える。例えば、

data Foo = Foo Int Double

というデータ型を定義したとして、これに対して辞書式順序を実装したいとしよう。Ordering のモノイド演算を使えば、

instance Ord Foo where
  compare (Foo a b) (Foo c d) = compare a c <> compare b d

と実装できる。（これが辞書式順序になっていることはちょっと考えればわかる）

この程度なら deriving を使えばいいかもしれない。ただ、フィールドの一部の順序を独自に定めたい（その型の標準のOrdインスタンス以外で比較したい）場合など、 deriving が使えないが辞書式順序を定義したい場合には役に立つだろう。

辞書式比較はHaskellだけでなく色々な言語で有用なので、他の言語でもこのテクニック（モノイド演算）を使いたい、と思われるかもしれない。しかし、他の言語は大抵正格評価するので、Haskell版のコードをそのまま移植すると比較の際に不要な計算をしてしまう。やるとすれば、 && や || のような短絡評価する演算子を導入する必要があるだろう。

ちなみに、 Ordering って結局何なの？これがモノイドになるのには数学的なバックグラウンドがあるんじゃないの？という問いに対して答えを与えておこう。先ほど登場した First を使うと、例えば First String を使って

LT ↔︎ First (Just "LT")
EQ ↔︎ First Nothing
GT ↔︎ First (Just "GT")

を対応させられる（Ordering を First String へモノイドとして埋め込むことができる）。つまり Ordering は First モノイドの一種だと考えられる。

IOと逐次実行

IOアクションを順番に実行する、というのはモノイドっぽい。処理として、

『Aを実行した後にBを実行する』の後にCを実行する　と、
Aを実行した後に『Bを実行した後にCを実行する』を実行する

は明らかに同じだ（つまり、結合法則が成り立つ）。そして、「何もしない値」として「何もしないIOアクション」が条件を満たしている。

というわけで、 IO () はモノイドとなる。実際、 putStr "Hello " <> putStrLn "world" は正当なHaskellコードで、実行するとHello worldが表示される。

より一般に、 a がモノイドの時に IO a はモノイドとなる。実装は

m1 <> m2 = do x1 <- m1
              x2 <- m2
              return (x1 <> x2)

と思って良い。

（関連：Wizardモノイド

Gabriel Gonzalez氏の記事（ネタ元）：Haskell for all: The wizard monoid
- pythonissam氏による翻訳：wizard モノイド (翻訳)
@lotz氏による紹介：Wizardモノイドとその仕組み – Qiita

）

勘の良い方はお気づきだろうが、このモノイドの定義は別にIOである必要はなく、一般のモナドに対してこういう風な（中の値がモノイドだった時に順番に評価してくっつける）モノイドの定義ができる。詳しくは後述する。

（🤔「こいついっつも後述してるな……」）

その他

これまでに書いた例以外にもモノイドとなる演算はたくさんある。

集合の和集合
- Haskellの Data.Set の Set 型は和集合 (union) によるMonoidインスタンスが定義されている。
集合の共通部分も結合法則を満たすが、単位元に相当するものは「全体集合」なので「全体集合」を表現できないとモノイドにならない。
集合の対称差
ビット演算：and, or, xor
unit型 ()

このブログでも、先日のフィボナッチ数を高速に計算する記事で、 FibPair というモノイドを定義した。モノイドは身の回りに溢れている！

モノイドに関するアルゴリズム

HaskellでのMonoidインスタンスがたくさんあるのはわかったが、Monoidだとどういうことが嬉しいのか。連結演算子 <> を使いまわせるメリットはすでにあげた。別のメリットとしては、Monoid一般に適用できるアルゴリズムを使いまわせる、ということがある。

リスト等の畳み込み（fold）

リストの要素を全部くっつける、という操作を考える。この操作は、リストの要素がモノイドでさえあれば実装できる。

-- リストに関する fold
fold :: (Monoid a) => [a] -> a

Haskellには実際こういう関数が、 Data.Foldable に用意されている。ただし、型がもうちょっと一般化されていて、リスト以外のコンテナー型（例えば Array や Vector）に対しても適用できるようになっている。

foldl や foldr との違いは、要素をくっつけるのにモノイド演算を使うこと、モノイドには単位元があるので初期値を与える必要がないことである。

-- 例：リストモノイドのリストをくっつける
> fold [[1,2],[3,4,5]]
[1,2,3,4,5] 

-- 例：Sumモノイドのリストをくっつける
> fold [Sum 1,Sum 3,Sum (-2)]
Sum {getSum = 2}

関連して、 fold と map を組み合わせた関数 foldMap も用意されている。

-- リストに関する foldMap
foldMap :: (Monoid m) => (a -> m) -> [a] -> m

これを使うと、数のリストに対して fold (map Sum [1,3,-2]) とする代わりに foldMap Sum [1,3,-2] とできる。

とはいえ、数のリストの総和を計算するのに getSum (foldMap Sum [1,3,-2]) などと書くHaskellプログラマーはいない。sum :: (Num a) => [a] -> a というそのまんまズバリな関数が用意されているのだから。

他にも、リストモノイドからなるリストを連結したかったら concat :: [[a]] -> [a] があるし、Product モノイド（数の積）に関しては product :: (Num a) => [a] -> a がある。All モノイド（Bool の &&）に関しては and :: [Bool] -> Bool が、Any モノイド（Bool の ||）に関しては or :: [Bool] -> Bool が用意されている。

この記事で挙げた他のモノイドに関して言えば、 First モノイドに関する fold に近いのは head, Last モノイドに関する fold に近いのは last である。ただし、head, last の返す型は Maybe a ではなく a で、リストが空の場合にはエラーが発生する。

同様に、 Max モノイドには maximum が、 Min モノイドには minimum が近いが、これらもリストが空の場合にはモノイドとしての単位元（型の最小値、最大値）を返すのではなく、エラーを発生させる。

繰り返し乗算

数の n 乗を計算するとき、どういうふうな計算方法を使うだろうか？

アルゴリズムに詳しい人なら、愚直に \((\cdots(((a \times a) \times a) \times a) \times \cdots) \times a\) とするより、指数を2進展開して計算する方が乗算回数が少なくて済む、と知っているだろう。

このアルゴリズム（指数を2進展開）を適用できる条件は、演算が結合的であることだけなので、数の掛け算に限らず任意のモノイドに一般化できる。

Haskellの場合は、このアルゴリズムで「モノイドを n 乗する」関数は Data.Semigroup に

stimesMonoid :: (Integral b, Monoid a) => b -> a -> a

という関数が用意されているので、それを使うことができる。（将来的には mtimes という関数がMonoidクラスに追加されるかもしれない）

ただ、指数を2進展開して演算回数を減らすアルゴリズムは、効果的な場合とそうでない場合があるので注意が必要だ。

例えば、足し算に関するモノイドにおいては、モノイドとしての n 乗というのはすなわち数としての n 倍なわけで、繰り返しモノイド演算（足し算）をしなくても、掛け算をすれば一発で計算できる。

別の例として、先日このブログに書いたフィボナッチ数関連の競プロ問題を解いてみた話では行列の特性多項式がわかっていたので、大きな n に対して繰り返し自乗するよりも多項式除算を使う方が効率的だった。

さらに別の例として、 First モノイドは任意の元 x に対して x <> x = x となる（このような性質を冪等（べきとう） (idempotent) という）。その場合、 x の n 乗は

\(n=0\) の場合、単位元
\(n\ge 1\) の場合、 x 自身

と実装できる。First のほか、これまでに挙げたモノイドの中では Last, All, Any, Max, Min, Ordering などが冪等である。

まとめると、「指数を2進展開して n 乗を計算する」アルゴリズムは任意のモノイドに適用できるが、考えているモノイドに対して本当にそのアルゴリズムが効果的かは一考するべきである。

なお、Semigroupクラスの stimes やMonoidクラスに将来追加されるかもしれない mtimes 関数は、クラス実装者がモノイドの特性に応じて効率的な実装を与えているはずなので、モノイドを利用する側は stimes を使っておけば良い。

Writerモナド

Writerモナドは、複数のアクションで産出された値を結合するのにMonoidクラスの演算を使う。文字列やリストなら連結されるし、Sumモノイドを使えば tell に渡した値が加算されて出てくる。

> runWriter (tell (Sum 42) >> tell (Sum 143) >> return "Hello")
("Hello",Sum {getSum = 185})

😹「ようやく Sum モノイドを使って嬉しい場面が出てきたよぅ……！」

まあWriterモナドはスペースリークを引き起こすとかいうので、真面目なコードで使っている人は少ないかもしれないが……。

🙀

でも最近スペースリークを引き起こさないWriterモナドが transformers に入ったらしいから、使える場面が増えていくかもしれない。あと関連するモナドとしてAccumモナドというものもあるらしい。

モノイドから新しいモノイドを構成する

SumやProductの存在意義

これまでに紹介した種々のモノイドを、畳み込みなどの「モノイドに関するアルゴリズム」に適用できる。ただ、畳み込み演算に関しては sum や product, and, or, concat など、それぞれのモノイド演算に特化したものが提供されていることが多い。繰り返し乗算も、足し算の場合は n 倍すれば良いだけだし、掛け算ならべき乗 ^ が既に用意されている。All や Any には繰り返し乗算を適用する意味がない。

こういう状況で、 Sum や Product, All や Any などのnewtype wrapperは本当に存在意義があるのだろうか。Writerモナドで使える、というだけでは理由として弱いのではないだろうか。

筆者なりの答えを述べよう。これらnewtype wrapperの真価が発揮されるのは、「モノイドを組み合わせて新しいモノイドを構成する」場合である。

例えば、整数のリスト xs :: [Int] から、和と最大値の両方を計算したいとしよう。別々に計算する

(sum xs, maximum xs)

か、手でfoldl/foldrを呼ぶ

foldl' (\(s, m) x -> (s + x, max m x)) (0, minBound) xs

か……。別々に計算するのでは、他の関数から返ってきたリストを処理する場合に一旦変数に束縛するのが手間だ。手でfoldl/foldrを呼ぶのは、関数と初期値を定義するのが手間である。

そんな時は、モノイドの力を使って

foldMap (\x -> (Sum x, Max x)) xs

と書けば良い。簡潔！（結果を取り出すときに getSum や getMax を使う手間はあるが）

何をしたかというと、Sum Int と Max Int という2つのモノイドを組み合わせて新しいモノイド (Sum Int, Max Int) を作ったのである。

既存のモノイドを組み合わせて、その場の問題に応じた新しいモノイドを作る。Sum や Max といったnewtype wrapperに価値があるとすれば、そういう「既存のモノイド」としての価値、建築材料としての価値であろう。

今の例では、タプル型 (,) に既存のモノイドを埋め込んで新しいモノイドを作った。また、これまでにモノイドの例のうち、Maybe 型や IO 型は既存のモノイドを入れることによって新しいモノイドを作ることができた。このように、既存のモノイドから新しいモノイドを構成する方法をいくつか見ておこう。

タプル

複数のモノイドを組み合わせる、という場合にはタプル型を使う。（数学オタク風に言えば、モノイドの直積だ）

これらは、要素ごとにモノイド演算を適用する。細かい説明は不要だろう。GHC 8.6時点での標準ライブラリー (base 4.12.0.0) では、5要素のタプルまでMonoidインスタンスが定義されているようだ。

instance (Monoid a, Monoid b) => Monoid (a, b) where
  (x, y) <> (x', y') = (x <> x', y <> y')
  mempty = (mempty, mempty)

instance (Monoid a, Monoid b, ..., Monoid e) => Monoid (a, b, c, d, e) where
  ...

関数

関数の返り値の型がモノイドだった場合、「2つの関数に同じ値（引数）を渡して、それぞれ帰ってきた値をくっつける」という操作によって関数をモノイドにできる。つまり、 a -> b という関数型は、 b がモノイドだった場合に

instance (Monoid b) => Monoid (a -> b) where
  f <> g = \x -> f x <> g x
  mempty = \x -> mempty

という風にモノイドにできる。

Dual

数や Bool に関してモノイドの定義の仕方が複数ある、と書いたが、よく考えたら文字列だってモノイドの定義の仕方は複数ある。

"foo" という文字列と "bar" という文字列のくっつけ方は "foobar" だけじゃなくてその逆順、 "barfoo" もアリだ。「文字列を逆順にくっつける」という演算もモノイドの性質を満たす。

別の例で言えば、 Endo の関数合成だって定義は f . g と g . f の2通り考えられる。

もっと一般化して、モノイドがあった時に左右を入れ替えて演算する、という操作によって新たなモノイドを構成できる。

こういう「左右を入れ替える」ことによって新たなモノイドを構成する方法は、Haskellでは Dual という名前のnewtype wrapperで用意されている。

それを使うと、文字列の結合の左右を入れ替えるモノイドは Dual String となるし、関数合成の左右を入れ替えるモノイドは Dual (Endo a) と書ける。

例：

> "foo" <> "bar"
"foobar"
> Dual "foo" <> Dual "bar"
Dual {getDual = "barfoo"}

モナドとモノイドからモノイドを作る: Ap

モノイドの例として「IOと逐次実行」を挙げたが、ああいうモノイドはIOモナドに限らず、任意のモナドで定義できる。実際、標準ライブラリー (base) で定義されているモナドのうち、

Monoid a => Monoid (ST s a)
Monoid a => Monoid (Identity a)
Monoid b => Monoid (a -> b)
Monoid a => Monoid (Maybe a) （注意：現在のGHCでは、より一般化して Semigroup a => Monoid (Maybe a) となっている。後述）

に関して、IOと同様の do x <- m1 ; y <- m2 ; return (x <> y) によるモノイドの定義がされている。（Maybe と a -> b に関しては個別に取り上げた）

一方、リスト型 [a] のモノイドの定義はリストの連結であって、リストモナドとしての逐次実行ではない。例えば、 ["a","b"] <> ["c","d","e"] の計算結果は ["a","b","c","d","e"] であって、モナドとして逐次実行した

do x1 <- ["a","b"]
   x2 <- ["c","d","e"]
   return (x1 <> x2)
= ["ac","ad","ae","bc","bd","be"]

ではない。それでも、newtype wrapperを書けば、リストモナドとしての逐次実行を使ったモノイドを作ることができる。

さて、「モナド m とモノイド a に対して m a をモノイドにできる」という性質に効いているのは、「モナド」というよりは m が「アプリカティブ関手」であるという性質である。実際、アプリカティブであれば m a のモノイド演算を (<>) = liftA2 (<>) によって定義できる。

一般のアプリカティブ関手 f とモノイド a があった時に f a に liftA2 (<>) によりモノイド構造を入れるnewtype wrapperは、 Ap という名前で提供されている。型引数の順番は Ap f a となる。（Ap が追加されたのはbase-4.12.0.0以降で、つい最近だ）

例えば、モノイドを要素とするリストに対して、（リストの連結ではない）リストモナドとしてのMonoidインスタンスが欲しければ、 Ap [] a とすれば良い。["a","b"] <> ["c","d","e"] を計算するとリストとしての連結が行われて ["a","b","c","d","e"] が帰ってくるが、 Ap ["a","b"] <> Ap ["c","d","e"] を計算するとモナドとして

do x1 <- ["a","b"]
   x2 <- ["c","d","e"]
   return (x1 <> x2)

が計算されて Ap ["ac","ad","ae","bc","bd","be"] が帰ってくる。

【2月13日追記】一般のアプリカティブ関手をモノイドにする（モノイドをアプリカティブ関手で持ち上げる） Ap は、deriving viaの論文で「deriving viaがあると嬉しい例」として取り上げられているようだ（ただし論文中では Ap という名前ではなく、 App と呼ばれている）。 https://www.kosmikus.org/DerivingVia/deriving-via-paper.pdf

半群 (Semigroup)

せっかくモノイドの話をしたので、関連する概念として半群 (semigroup) の話もしておこう。

モノイドは「結合的な二項演算」と「単位元」から成り立っていたが、半群は「結合的な二項演算」から成る。単位元は必ずしも必要ではない。つまり、半群はモノイドの一般化で、モノイドは漏れなく半群である。

Haskellにおいては半群を表す型クラスは Semigroup という名前で、大雑把に言うと

class Semigroup a where
  (<>) :: a -> a -> a

と定義されている。そう、この記事で散々モノイド演算と称してきた <> は Monoid クラスではなく Semigroup クラスで定義されていたのだ！ Monoidクラスは当然 Semigroup クラスのサブクラスとして、

class (Semigroup a) => Monoid a where
  mempty :: a

という風に定義されている。「モノイドは半群である」ことが、型クラスの階層として表現されている。

半群はモノイドの一般化なので、半群の例としてはこれまでに挙げてきたモノイド全てが該当する。だが、わざわざ一般化するということは、一般化して嬉しい場合、つまりモノイドの枠組みでは扱えないが半群の枠組みでは扱える対象というのがあるはずだ。

というわけで、まずはモノイドになるとは限らないが半群となる例を見ていこう。（ちなみに、「モノイドから新しいモノイドを構成する」で説明した奴らは全部半群に対しても適用できて、結果として半群が得られる）

半群の例（特に、モノイドになるとは限らないもの）

NonEmpty: 空ではないリスト

「空でないリスト」の集まりは、連結演算に関して半群となる。リスト連結演算に関する単位元は空リストなので、「空でないリスト」の集まりは単位元を持たない。

Haskellでは「空でないリスト」型は、Data.List.NonEmptyモジュールの NonEmpty 型として用意されている。

Max, Min: 大きい方と小さい方

max, min関数は何もしなくても結合法則を満たすが、モノイドとなるには単位元として最小値、最大値が必要なのだった。なので、max関数を演算とする Max Integer という型はモノイドにはならない。

しかし、半群の定義に単位元は必要ない。よって、Max Integer や Min Integer などの型は半群になる。

> Max 123 <> Max 456 :: Max Integer
Max {getMax = 456}

First, Last (Data.Semigrop)

先に紹介した First, Last は Maybe のエイリアス (newtype wrapper) だった、それとは異なる First, Last がData.Semigroupモジュールに定義されている。Data.Semigroupの First, Last は Maybe ではなく、パラメーターとして与えられた型のnewtypeである。つまり

newtype First a = First { getFirst :: a }
instance Semigroup (First a) where
  First x <> First _ = First x

newtype Last a = Last { getLast :: a }
instance Semigroup (Last a) where
  Last _ <> Last y = Last y

と定義されている。比較：

> Data.Monoid.First (Just 123) <> Data.Monoid.First (Just 456)
First {getFirst = Just 123}
> Data.Semigroup.First 123 <> Data.Semigroup.First 456
First {getFirst = 123}

Void

自明な例だが、「値を持たない型」Void は半群となる。値がないので、演算 <> の定義について悩むこともない。

一方、型がモノイドになるためには、単位元という形で必ず一個以上値を持たなければならないので、 Void はモノイドにはならない。

集合の共通部分

ある集合 \(X\) の部分集合全体 \(\mathcal{P}(X)\)、という集まりは共通部分 \(\cap\) に関して半群となる。共通部分 \(\cap\) という演算の単位元は、全体集合 \(X\) である。

ただ、Haskellでいう Data.Set の Set 型のような、「有限部分集合」を表す型の場合は、要素として取りうる値の集合が有限でないと全体集合を表現できない。つまり、Set 型は共通部分に関して必ずしもモノイドにはならない。

半群とMaybeとモノイド

先ほどMaybeがモノイドの例だと述べたときに、モノイド構造の定義を「Maybe の中身もモノイドだと仮定して、 Just x <> Just y = Just (x <> y) とする。」とした。

この際、実は Maybe の中身の型が単位元を持っている必要はなく、結合的な演算、つまり半群の構造を持ってさえいれば良い。Maybe の中身の型 a が（モノイドじゃない）半群に過ぎなくても、Maybe a はちゃんとモノイドになってくれる。

よって Maybe のモノイドの定義は

class (Semigroup a) => Semigroup (Maybe a) where
  Nothing <> y = y
  Just x <> Nothing = Just x
  Just x <> Just y = Just (x <> y)
class (Semigroup a) => Monoid (Maybe a) where
  mempty = Nothing

となる。

こうしてみると、 Maybe a は、単位元を必ずしも持たない半群 a に対して単位元を「付け加えて」モノイドにしたものだと考えられる。

なお、もとの半群 a が単位元を持っていた場合、a の単位元を Just で埋め込んだもの Just mempty は Maybe a の単位元とは異なる元になる（Maybe a の単位元はあくまで Nothing）。

こうしてみると、この記事で挙げた「モノイドの例」と「必ずしもモノイドではない半群の例」を、 Maybe を介して結びつけることができる。

例：Maybe (NonEmpty a) はモノイドであり、 [a] と同型である（面倒なHaskellオタクのために一言断っておくと、ボトムは無視する）。

例：Maybe (Data.Semigroup.First a) はモノイドであり、 Data.Monoid.First a と同型である（この場合はどちらも Maybe a と実態が同じだが、モノイド演算のボトムに関する挙動が異なる）。

例：Maybe Void はモノイドであり、unit型（単位モノイド）と同型である（例によってボトムはry）。

例：半群 Max Integer はモノイドにならないが、 Maybe (Max Integer) はモノイドになる。ちなみに Max (Maybe Integer) はモノイドにならない。Maybe Integer 自体は < に関する最小元 Nothing を持つが、Bounded のインスタンスではないからだ。

Maybe を使うと、Max モノイドや Min モノイドに関して、minBound / maxBound の代わりにわかりやすい単位元を与えることができる。つまり、Int 型の max 関数に関するモノイドであって、単位元が \(-2^{63}\) のようなよくわからない値ではなく、 Nothing というわかりやすい値となるようなモノイドを Maybe (Max Int) と構成することができる：

> fold [] :: Max Int
Max {getMax = -9223372036854775808}
> fold [] :: Maybe (Max Int)
Nothing

（圏論オタクのためにもう一言述べておくと、「モノイドの圏」から「半群の圏」への忘却関手の左随伴が Maybe となっている。）

半群、モノイド、じゃあ次は？

😼「半群（の定義）を拡張するとモノイドとなる。となると、次はモノイドを拡張して、群の話が来るのかな？わくわく」

モノイドは半群の拡張（定義の際に単位元を要請する）と思うことができる。さらに、群はモノイドの拡張（定義の際に逆元を要請する）と思うことができる。代数構造大好な読者諸氏は、「モノイドと半群の話をしたのなら、群の話をしてもいいのでは」と思われるかもしれない。

しかし、モノイドと半群は比較的近かったが、モノイドと群は結構遠い（大幅に異なる）。どういうことか。

ここではモノイドの例をたくさん挙げたが、その中で群の例になるようなのはunit型 ()、Sum、集合の対称差とビット演算の xor くらいしかない（Product も、もとが体であって、0を扱わないと約束するのであれば群となる）。他は全て、モノイドの例ではあっても群の例ではない。

また、半群は Maybe をかますことによって単位元を加え、簡単にモノイドにできた。しかし、モノイドに逆元を加えて群にする標準的で簡単な方法はない。一般のモノイドを群にするには、「逆元」を大量に加えて、それを関係式で割る、という作業が必要になる（数学的な操作としては構成できても、プログラムとして実装できるか怪しい。自由モノイド／自由群くらいならともかく）。

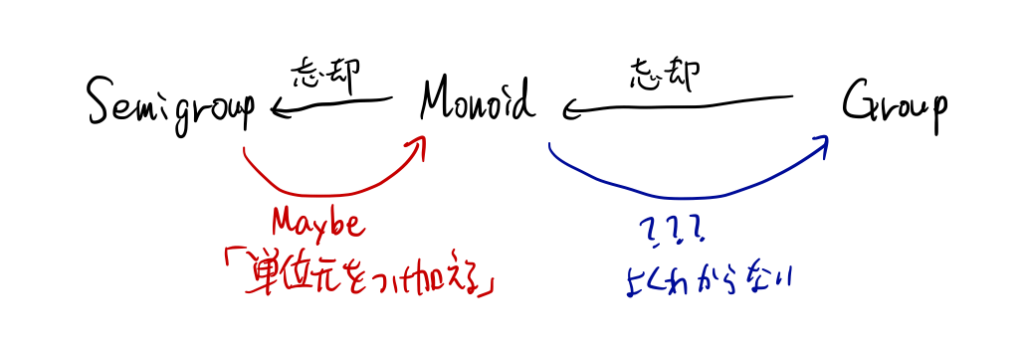
したがって、半群とモノイドは近いので同じ記事で取り扱う意義はあるが、モノイドと群は毛色が違うので、プログラミングにおける応用を考えるなら別々に論じるべきである。

（それにほら、Haskellのbaseに Data.Monoid はあっても Data.Group はないし…）

半群やモノイドから話を広げるなら、半環とか、あるいはsemigroupoidや圏 (category) の方がお手頃だろう。

歴史の話：Semigroup-Monoid Proposal以前（GHC 8.2まで）

この記事のここまでの部分はGHC 8.4以降 (base 4.11.* 以降）を対象に書かれており、GHC 8.2まで（base 4.10.* まで）に対してはそのまま当てはまらない。

まず、GHC 8.2の時点ではSemigroupはMonoidのスーパークラスではなかった。そして、Data.SemigroupとData.Monoidに、異なる2つの <> が定義されていた。

-- GHC 8.2 まで

module Data.Semigroup where

class Semigroup a where
  (<>) :: a -> a -> a

module Data.Monoid where

class Monoid a where
  mappend :: a -> a -> a
  mempty :: a

(<>) :: Monoid a => a -> a -> a
(<>) = mappend

Haskellの標準ライブラリーに先にあったのは Monoid クラスで、後から Semigroup を入れたために（互換性を壊さないように）このような事態になっていたわけだ。これをあるべき姿 — Semigroup が Monoid のスーパークラスである — に変える提案は Semigroup-Monoid Proposal と呼ばれており、 GHC 8.4 でそれが適用された。

Semigroup-Monoid Proposalに関する、山本和彦氏による記事：あなたの知らないSemigroupの世界 – あどけない話

🤔.oO（Functor, Applicative, Monad 周りでも似たような話があったな……）

まあ、GHC 8.2 の段階で、大抵の Monoid のインスタンスは大抵 Semigroup のインスタンスでもあったので、モノイドを使う側からすればどちらの <> を使っても問題はなかったはずだ。

一つ、Semigroup-Monoid Proposalが適用されたことで不要となったnewtype wrapperを紹介しよう。

Maybe a がモノイドとなるには a は半群であれば良い（モノイドである必要はない）というのはすでに説明した通りだ。しかし、Semigroup は元々標準ライブラリーになかったので、従来は Maybe a の Monoid インスタンスの定義で instance (Monoid a) => Monoid (Maybe a) と、 a も Monoid であることを要求していた。この条件を安易に Semigroup a に変えてしまうと、既存のコードが壊れてしまうかもしれない。

しかしそれでは Maybe (Max Integer) が Monoid のインスタンスとなってくれない（Semigroup のインスタンスにはできる）。例：

> fold [] :: Maybe (Max Integer) 

<interactive> :6:1: error:
     • No instance for (Bounded Integer) arising from a use of ‘fold’
     • In the expression: fold [] :: Maybe (Max Integer)
       In an equation for ‘it’: it = fold [] :: Maybe (Max Integer)

そこで導入された Maybe のnewtype wrapperが Option 型である。Option 型の Semigroup / Monoid インスタンスの定義は概ね Maybe と同じだが、ただ一点、 Monoid (Option a) の条件が Monoid a ではなく Semigroup a であることが異なる。

instance (Semigroup a) => Semigroup (Maybe a) where
  (<>) = ...
instance (Monoid a) => Monoid (Maybe a) where
  mappend = ...
  mempty = Nothing

newtype Option a = Option { getOption = Maybe a }
instance (Semigroup a) => Semigroup (Option a) where
  (<>) = ...
instance (Semigroup a) => Monoid (Option a) where
  mappend = (<>)
  mempty = Option Nothing

使用例：

> fold [] :: Option (Max Integer)
Option {getOption = Nothing} 

> -- Semigroup としては Maybe も Option も同等
> Just (Max 123) Data.Semigroup.<> Just (Max 456) :: Maybe (Max Integer)
Just (Max {getMax = 456}) 
> Option (Just (Max 123)) Data.Semigroup.<> Option (Just (Max 456)) :: Option (Max Integer)
Option {getOption = Just (Max {getMax = 456})}

GHC 8.4 では無事 Semigroup-Monoid Proposal が適用され、 Monoid (Maybe a) の条件として Semigroup a を課すことになんの躊躇もなくなったので、 Option 型を使う必要はなくなった。

あと GHC 8.4 以降では不要となったnewtype wrapperとして WrappedMonoid というものもあったが、説明は省略する。

Haskell中上級者向けの注意点：演算子の結合性

モノイドや半群は a <> (b <> c) == (a <> b) <> c （結合法則）を満たすもののことだった。数学的には「a <> (b <> c) と (a <> b) <> c は同じ」と言って良いのだが、プログラミングをする上ではもう少し考えることがある。そう、a <> (b <> c) と (a <> b) <> c の結果の値は同じでも、計算の過程、消費する時間やメモリの量が同じとは限らない。

例えば、リストの連結では (xs <> ys) <> zs よりも xs <> (ys <> zs) の方が効率が良い。それを反映して、リスト専用の連結演算子 ++ は右結合、つまり xs ++ ys ++ zs が xs ++ (ys ++ zs) と解釈されるように定義されている。

他の例を挙げると、 Data.Monoid.First（Maybe の別名）に関しても a <> (b <> c) の方が良い。Ordering も同様だ。

逆に、 Data.Monoid.Last に対しては (a <> b) <> c の方が良い。

一方、 Sum Int のように、 (a <> b) <> c と a <> (b <> c) で効率が変わらなさそうなものもある。

ではモノイドの連結演算子 <> はどう定義されているのかというと、これは右結合、つまり xs <> ys <> zs と書いたら xs <> (ys <> zs) と解釈するように定義されている。よって、リスト（String を含む）、Ordering などのよく使うモノイドに関しては何も考えずに <> を使って良い。

というわけで、Haskell中上級者は、「これはモノイドだから結合法則が成り立つけど、どっちの方が効率が良いか（あるいは、どっちでもいいのか）」を意識できると良い。

なお、結合性が重要ではないモノイドの場合は、並列性の観点から考えて適当にバラしてくれた方が良いかもしれない。つまり、 x <> y <> z <> w を (x <> y) <> (z <> w) と計算すると嬉しいかもしれない。この辺の話はこの記事では扱わない。

まとめ

モノイドは
　いたるところに
　　現れる

雑記帳

人生やっていき

Haskellerのためのモノイド完全ガイド

モノイドとは

HaskellとMonoidクラス

Haskellと文字列と連結演算子

モノイドの例

文字列 (String, Text, ByteString)

リスト

数：足し算と掛け算 (Sum, Product)

Bool: 論理積と論理和 (All, Any)

自分自身への関数 `a -> a` (Endo)

Maybe, First, Last

Max, Min: 大きい方と小さい方

Ordering: 辞書式順序

IOと逐次実行

その他

モノイドに関するアルゴリズム

リスト等の畳み込み（fold）

繰り返し乗算

Writerモナド

モノイドから新しいモノイドを構成する

SumやProductの存在意義

タプル

関数

Dual

モナドとモノイドからモノイドを作る: Ap

半群 (Semigroup)

半群の例（特に、モノイドになるとは限らないもの）

NonEmpty: 空ではないリスト

Max, Min: 大きい方と小さい方

First, Last (Data.Semigrop)

Void

集合の共通部分

半群とMaybeとモノイド

半群、モノイド、じゃあ次は？

歴史の話：Semigroup-Monoid Proposal以前（GHC 8.2まで）

Haskell中上級者向けの注意点：演算子の結合性

まとめ